
This course is run at the The University of Nottingham within the School of Computer Science & IT. The course is run by Graham Kendall (EMAIL : gxk@cs.nott.ac.uk)
A blind search (also called an uninformed search) is a search that has no information about its domain. The only thing that a blind search can do is distinguish a non-goal state from a goal state.
Consider the following, simplified map of Romania

Assume you are currently in Arad and we want to get to Bucharest. If we produce
a search tree, level 1 will have three states; Zerind, Sibiu and Timisoara.
A blind search will have no preference as to which node it should explore first
(later we will see that we can develop search strategies that incorporate some
intelligence).
You may wonder why we should use a blind search, when we could use a search
with some built in intelligence. The simple answer is that there may not be
any information we can use. We might just be looking for an answer and won't
know we've found it until we see it.
But it is also useful to study these uninformed searches as they form the basis
for some of the intelligent searches that we shall be looking at later.
The blind searches we are about to consider only differ in the order in which we expand the nodes but, as we shall see, this can have a dramatic effect as to how well the search performs.
Using a breadth-first strategy we expand the root level first and then we expand
all those nodes (i.e. those at level 1) before we expand any nodes at level
2.
Or to put it another way, all nodes at level d are expanded before any
nodes at level d+1.
In fact, if you (as suggested) worked through the search algorithm on the last
page (Defining and Implementing a Search) you will
have seen a breadth first search in action.
This is because we can implement a breadth first search by using a queuing function
that adds expanded nodes to the end of the queue.
Therefore, we could implement a breadth-first search using the following algorithm
Function BREADTH-FIRST-SEARCH(problem) returns a solution or
failure
Return GENERAL-SEARCH(problem, ENQUEUE-AT-END)
I have produced a powerpoint presentation to show breadth
first search. It might also be worth looking at the powerpoint
guidelines I gave you earlier.
You will recall that we defined four criteria that we are going to use to measure various search strategies; these being completeness, time complexity, space complexity and optimality. In terms of those, breadth-first search is both complete and optimal. Or rather, it is optimal provided that the solution is also the shallowest goal state or, to put it another way, the path cost is a function of the depth.
But what about time and space complexity?
To measure this we have to consider the branching factor, b; that is every state
creates b new states.
The root of our tree has 1 state. Level 1 produces b states and the next level
produces b2 states. The next level produces b3 states.
Assuming the solution is found a level d then the size of the tree is
1 + b + b2 + b3 + ... + bd
(Note : as the solution could be found at any point on the d level then the search tree could be smaller than this).
This type of exponential growth (i.e. O(bd) ) is not very healthy.
You only have to look at the following table to see why.
|
Depth
|
Nodes
|
Time
|
Memory
|
|
0
|
1
|
1 millisecond
|
100 kbytes
|
|
2
|
111
|
0.1 second
|
11 kilobytes
|
|
4
|
11,111
|
11 seconds
|
1 megabyte
|
|
6
|
106
|
18 minutes
|
111 megabytes
|
|
8
|
108
|
31 hours
|
11 gigabytes
|
|
10
|
1010
|
128 days
|
1 terabyte
|
|
12
|
1012
|
35 years
|
111 terabytes
|
|
14
|
1014
|
3500 years
|
11,111 terabytes
|
Time and memory requirements for breadth-first search, assuming a branching factor of 10, 100 bytes per node and searching 1000 nodes/second
We can make some observations about these figures
It is true to say that breadth first search can only be used for small problems. If we have larger problems to solve then there are better blind search strategies that we can try.
We have said that breadth first search finds the shallowest goal state and
that this will be the cheapest solution so long as the path cost is a function
of the depth of the solution. But, if this is not the case, then breadth first
search is not guaranteed to find the best (i.e. cheapest) solution.
Uniform cost search remedies this.
It works by always expanding the lowest cost node on the fringe, where the cost
is the path cost, g(n). In fact, breadth first search is a uniform cost search
with g(n) = DEPTH(n).
Consider the following problem.
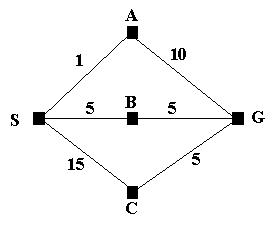
We wish to find the shortest route from S to G; that is S is the initial state
and G is the goal state. We can see that SBG is the shortest route but if we
let breadth first search loose on the problem it will find the path SAG; assuming
that A is the first node to be expanded at level 1.
But this is how uniform cost search tackles the problem.
We start with the initial state and expand it. This leads to the following tree
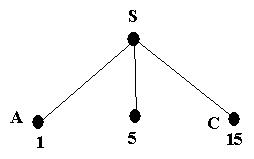
The path cost of A is the cheapest, so it is expanded next; giving the following tree

We now have a goal state but the algorithm does not recognize it yet as there
is still a node with a cheaper path cost. In fact, what the algorithm does is
order the queue by the path cost so the node with cost 11 will be behind node
B in the queue.
Node B (being the cheapest) is now expanded, giving
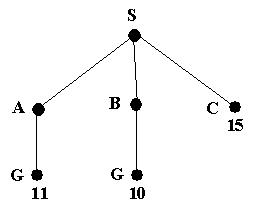
A goal state (G) will now be at the front of the queue. Therefore the search will end and the path SBG will be returned.
I have produced a powerpoint presentation which shows the above search. It might also be worth looking at the powerpoint guidelines I gave you earlier.
In summary, uniform cost search will find the cheapest solution provided that the cost of the path never decreases as we proceed along the path. If this requirement is not met then we never know when we will meet a negative cost. The result of this would be a need to carry out an exhaustive search of the entire tree.
Depth first search explores one branch of a tree before it starts to explore another branch. It can be implemented by adding newly expanded nodes at the front of the queue.
Using the general search algorithm we can implement it as follows.
Function DEPTH-FIRST-SEARCH(problem) returns a solution or failure
Return GENERAL-SEARCH(problem, ENQUEUE-AT-FRONT)
Pictorially, a depth first search can be shown as follows
I have produced a powerpoint presentation to show depth first search. It might also be worth looking at the powerpoint guidelines I gave you earlier.
We can make the following comments about depth first search
The choice of the depth parameter can be an important factor. Choosing a parameter that is too deep is wasteful in terms of both time and space. But choosing a depth parameter that is too shallow may result in never reaching a goal state.
As long as the depth parameter, l (this is lower case L, not the digit one), is set "deep enough" then we are guaranteed to find a solution if it exists. Therefore it is complete as long as l >= d (where d is the depth of the solution). If this condition is not met then depth limited search is not complete.
The space requirements for depth limited search are similar to depth first
search. That is, O(bl).
The time complexity is O(bl )
The problem with depth limited search is deciding on a suitable depth parameter.
If you look at the Romania map you will notice that there are 20 towns. Therefore,
any town is reachable from any other town with a maximum path length of 19.
But, closer examination reveals that any town is reachable in at most 9 steps.
Therefore, for this problem, the depth parameter should be set as 9. But, of
course, this is not always obvious and choosing a parameter is one reason why
depth limited searches are avoided.
To overcome this problem there is another search called iterative deepening
search.
This search method simply tries all possible depth limits; first 0, then 1,
then 2 etc., until a solution is found.
What iterative deepening search is doing is combining breadth first search and
depth first search.
I have produced a powerpoint presentation to show iterative deepening search. It might also be worth looking at the powerpoint guidelines I gave you earlier.
It may appear wasteful as it is expanding nodes multiple times. But the overhead
is small in comparison to the growth of an exponential search tree.
To show this is the case, consider this.
For a depth limited search to depth d with branching b the number of expansions is
1 + b + b2 + … + bd-2 + bd-1 + bd
If we apply some real numbers to this (say b=10 and d=5), we get
1 + 10 + 100 + 1,000 +10,000 + 100,000 = 111,111
For an iterative deepening search the nodes at the bottom level, d, are expanded
once, the nodes at d-1 are expanded twice, those at d-3 are expanded three times
and so on back to the root.
The formula for this is
(d+1)1 + (d)b+(d-1)b2 + … + 3bd-2 + 2bd-1 + 1bd
If we plug in the same numbers we get
6 + 50 + 400 + 3,000 + 20,000 + 100,000 = 123,456
You can see that, compared to the overall number of expansions, the total is not substantially increased.
In fact, when b=10 only about 11% more nodes are expanded for a breadth first
search or a depth limited node down to level d.
Even when the branching factor is 2 iterative deepening search only takes about
twice as long as a complete breadth first search.
The time complexity for iterative deepening search is O(bd) with the space complexity being O(bd).
For large search spaces where the depth of the solution is not known iterative deepening search is normally the preferred search method.
In this section we have looked at five different blind search algorithms. Whilst
these algorithms are running it is possible (and for some problems extremely
likely) that the same state will be generated more than once.
If we can avoid this then we can limit the number of nodes that are created
and, more importantly, stop the need to have to expand the repeated nodes.
There are three methods we can use to stop generating repeated nodes.
The three methods are shown in increasing order of computational overhead in
order to implement them.
The last one could be implemented via hash tables to make checking for repeated
states as efficient as possible.
This is a summary of the five search methods that we have looked at. In the
following table the following symbols are used.
B = Branching factor
D = Depth of solution
M = Maximum depth of the search tree
L = Depth Limit
| Evaluation | Breadth First | Uniform Cost | Depth First | Depth Limited | Iterative Deepening |
| Time |
BD
|
BD
|
BM
|
BL
|
BD
|
| Space |
BD
|
BD
|
BM
|
BL
|
BD
|
| Optimal? |
Yes
|
No
|
No
|
No
|
Yes
|
| Complete? |
Yes
|
Yes
|
No
|
Yes, ifL>=D
|
Yes
|
Last Updated : 27 Sep 2001