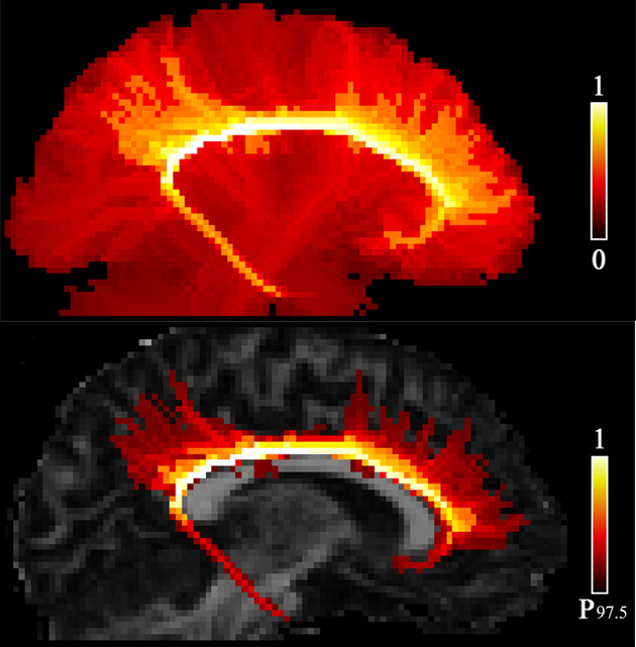
Methods by which to model white matter tracts using brain tractography commonly use curve propagation from a seed to imply connectivity in voxels. Additional, underdeveloped, approaches involve quantification of strength in the connections between all voxels and the seed using graph theory. Inherent limitations occur in existing methods, such as unlikely connections being identified in fibre crossing regions by assignment of high connection strengths to all crossing populations.
Our approach for robustly propagating through fibre crossings, described by the Q-ball derived orientation distribution functions involves treating each voxel as a graph node and neighboring pixels connected by arcs. These arcs are weighted with structural and diffusivity features.
To account for crossing fibre populations within a voxel, complex ODFs are decomposed into representations of single-fibre populations and a multigraph created. This is searched exhastively to find the strongest paths and assign connectivity strengths between a seed and other voxels. After comparison with existing methods, the method developed improves on connection strength in fibre crossing regions, and reduces the strength of anatomically implausible paths.
Citations: [·]