The language of a DFA

To each DFA $A$ we associate a language $L(A)\subseteq \Sigma^*$. To see whether a word $w\in L(A)$ we put a marker in the initial state and when reading a symbol forward the marker along the edge marked with this symbol. When we are in an accepting state at the end of the word then $w\in L(A)$, otherwise $w\notin L(A)$.

In the example above we have that $0\notin L(B)$, $101\in L(B)$ and $110\notin L(B)$. Indeed, we have

$$L(B) = \{ w \mid \textrm{$w$ contains the substring $01$} \}$$

To be more precise we give a formal definition of $L(A)$. First we define the extended transition function $\hat{\delta}\in Q\times \Sigma^* \to Q$. Intuitively, $\hat{\delta}(q,w)=q'$ if starting from state $q$ we end up in state $q'$ when reading the word $w$. Formally, $\hat{\delta}$ is defined by primitive recursion:

$$\hat{\delta}(q,\epsilon) = q$$ (1)

$$\hat{\delta}(q,xw) = \hat{\delta}(\delta(q,x),w)$$ (2)

Here $xw$ stands for a non empty word whose first symbol is $x$ and the rest is $w$. E.g. if we are told that $xw=010$ then this entails that $x=0$ and $w=10$. $w$ may be empty, i.e. $xw=0$ entails $x=0$ and $w=\epsilon$.

As an example we calculate $\hat{\delta}_B(q_0,101)=q_1$:

$$% latex2html id marker 4494\begin{array}{lcll} \ \hat{\del... ...& = & q_2 \ & \textrm{by (\ref{delta-hat-epsilon})} \end{array}$$

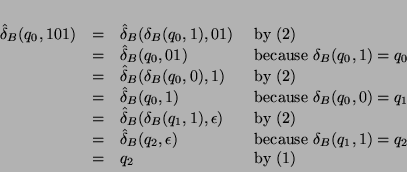
Using $\hat{\delta}$ we may now define formally:

$$L(A) = \{ w \mid \hat{\delta}(q_0,w)\in F\}$$

Hence we have that $101\in L(B)$ because $\hat{\delta}_B(q_0,101)=q_2$ and $q_2\in F_B$.