-
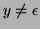
-
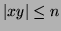
- for all
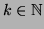 we have
we have
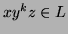 .
.
Proof: For a regular language ![]() there exists a DFA
there exists a DFA ![]() s.t.
s.t. ![]() . Let us assume that
. Let us assume that ![]() has got
has got ![]() states. Now if
states. Now if ![]() accepts a word
accepts a word ![]() with
with
![]() it must have visited a state
it must have visited a state
![]() twice:
twice:
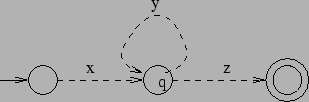
We choose ![]() s.t. it is the first cycle, hence
s.t. it is the first cycle, hence
![]() . We also
know that
. We also
know that ![]() is non empty (otherwise there is no cycle).
is non empty (otherwise there is no cycle).
Now, consider what happens if we feed a word of the form ![]() to
the automaton, i.e. s instead of
to
the automaton, i.e. s instead of ![]() it contains an arbotrary number
of repetetions of
it contains an arbotrary number
of repetetions of ![]() , including the case
, including the case ![]() , i.e.
, i.e. ![]() is just left
out. The automaton has to accept all such words and hence
is just left
out. The automaton has to accept all such words and hence
![]()
![]()