


Next: How to implement the
Up: How to implement a
Previous: How to calculate and
Let's have a look at the grammar  for arithmetical expressions
again.
for arithmetical expressions
again.
 where
where
We don't need the
 -sets in the moment because the empty word
doesn't occur in the grammar. For the nonterminal symbols we have
-sets in the moment because the empty word
doesn't occur in the grammar. For the nonterminal symbols we have
and now it is easy to see that most of the
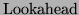 -sets agree,
e.g.
-sets agree,
e.g.
Hence the grammar 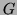 is not LL(1).
is not LL(1).
However, luckily there is an alternative grammar 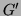 which defines the
same language:
which defines the
same language:
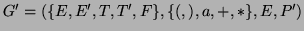 where
where
Since we have  -productions we do need the
-productions we do need the
 -sets.
-sets.
Now we calculate the
 -sets:
-sets:
Hence the grammar 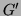 is LL(1).
is LL(1).



Next: How to implement the
Up: How to implement a
Previous: How to calculate and
Thorsten Altenkirch
2001-05-08
![]() for arithmetical expressions
again.
for arithmetical expressions
again.
![]() where
where
![]() which defines the
same language:
which defines the
same language:
![]() where
where