What is an NFA?

Nondeterministic finite automata (NFA) have transition functions which may assign several or no states to a given state and an input symbol. They accept a word if there is any possible transition from the one of initial states to one of the final states. It is important to note that although NFAs have a non-determistic transition function, it can always be determined whether or not a word belongs to its language ($w\in L(A)$). Indeed we shall see that every NFA can be translated into an DFA which accepts the same language.

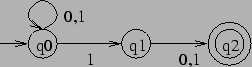
Here is an example of an NFA $C$ which accepts all words over $\Sigma=\{0,1\}$ s.t. the symbol before the last is $1$.

A nondeterministic finite automaton (NFA) $A=(Q,\Sigma,\delta,q_0,F)$ is given by:

1. A finite set of states $Q$,

2. A finite set of input symbols $\Sigma$,

3. A transition function $\delta \in Q\times\Sigma \to {\cal P}(Q)$,

4. A set of initial state $S \subseteq Q$,

5. A set of accepting states $F\subseteq Q$.

Hence, the only difference to DFAs are to have start staes instead of a single one and the type of the transition function. As an example we have that

$$C = (\{q_0,q_1,q_2\},\{0,1\},\delta_C,\{q_0\},\{q2\})$$

where $\delta_C$ so given by

$$\begin{array}{r\vert\vert c\vert c} \delta_C & 0 & 1 \h... ...q_1 & \{q_2\} & \{q_2\} \\ {*} q_2 & \{\} & \{\} \end{array}$$

Note that we diverge he slightly from the definition in the book, which uses a single initial state instead of a set of initial states. Doing so means that we can avoid introducing $\epsilon$-NFAs (see section 2.5 of the book).