To see whether a word
![]() is accepted by an NFA (
is accepted by an NFA (![]() we may have to use several marker. Initially we put one marker
on the initial state. Then each time when we read a symbol we look at
all the markers: we remove the old marker and put markers
at all the states which are reachable via an arrow marked with the
current input symbol (this may include the state which was marked in
the previously). Thus we may have to use several marker but it may
also happen that all markers disappear (if no appropriate arrows
exist). In this case the word is not accepted. If at the end of the
word any of the final states has a marker on it then the word is
accepted.
we may have to use several marker. Initially we put one marker
on the initial state. Then each time when we read a symbol we look at
all the markers: we remove the old marker and put markers
at all the states which are reachable via an arrow marked with the
current input symbol (this may include the state which was marked in
the previously). Thus we may have to use several marker but it may
also happen that all markers disappear (if no appropriate arrows
exist). In this case the word is not accepted. If at the end of the
word any of the final states has a marker on it then the word is
accepted.
E.g. consider the word ![]() (which is not accepted by
(which is not accepted by ![]() ). Initially
we have
). Initially
we have
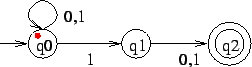
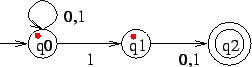
After reading ![]() we have to use two markers because there are two
arrows from
we have to use two markers because there are two
arrows from ![]() which are labelled
which are labelled ![]() :
:
Now after reading 0 the automaton has still got two markers, one of them in an accepting state:
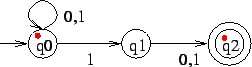
However, after reading the 2nd 0 the second marker disappears
because there is no edge leaving ![]() and we have:
and we have:
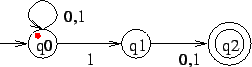
which is not accepting because no marker is in the accepting state.
To specify the extended transition function for NFAs we use an
generalisation of the union operation ![]() on sets. We define
on sets. We define ![]() to be the union of a (finite) set of sets:
to be the union of a (finite) set of sets:
As an example
We define
![]() with the
intention that
with the
intention that
![]() is the set of states which is
marked after having read
is the set of states which is
marked after having read ![]() starting with the initial markers given
by
starting with the initial markers given
by ![]() .
.
As an example we calculate
![]() which is
which is
![]() as we already know from playing with markers.
as we already know from playing with markers.
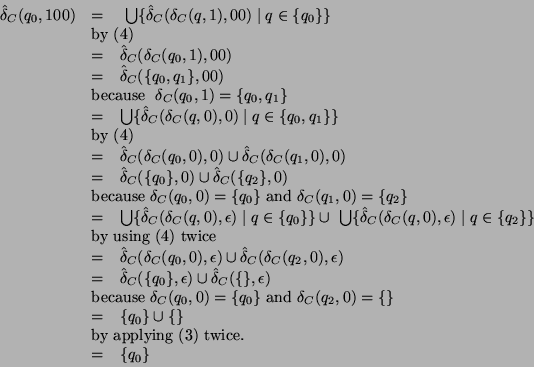
Using the extended transition function we define the language of an NFA as
This shows that
![]() because
because