DFAs can be viewed as a special case of NFAs, i.e. those for which the
the there is precisely one start state ![]() and the
transition function returns always one-element sets
(i.e.
and the
transition function returns always one-element sets
(i.e.
![]() for all
for all ![]() and
and
![]() ).
).
Below we show that for every NFA we can construct a DFA which accepts the same language. This shows that NFAs aren't more powerful as DFAs. However, in some cases NFAs need a lot fewer states than the corresponding DFA and they are easier to construct.
Given an NFA
![]() we construct the DFA
we construct the DFA
The basic idea of this construction (the subset construction)
is to define a DFA whose states are sets of states of the NFA. A final
state of the DFA is a set which contains at least a final state of the
NFA. The transitions just follow the active set of markers, i.e.
a state
![]() corresponds to having markers on all
corresponds to having markers on all ![]() and
when we follow the arrow labelled
and
when we follow the arrow labelled ![]() we get the set of states which
are marked after reading
we get the set of states which
are marked after reading ![]() .
.
As an example let us consider the NFA ![]() above. We construct a DFA
above. We construct a DFA ![]()
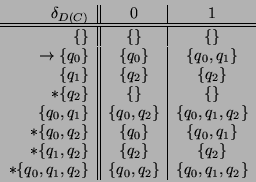
Looking at the transition diagram:
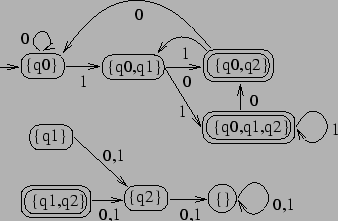
we note that some of the states (
![]() )
cannot be reached from the initial state, which means that they can be
omitted without changing the language. Hence we obtain the following
automaton:
)
cannot be reached from the initial state, which means that they can be
omitted without changing the language. Hence we obtain the following
automaton:
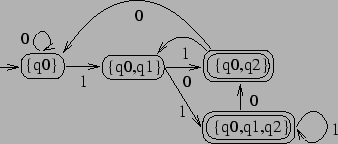
We still have to convince ourselves that the DFA ![]() accepts the same
language as the NFA
accepts the same
language as the NFA ![]() , i.e. we have to show that
, i.e. we have to show that
![]() .
.
As a lemma we show that the extended transition functions coincide:
The result of both functions are sets of states of the NFA
Proof: We show this by induction over the length of the word ![]() ,
let's write
,
let's write ![]() for the length of a word.
for the length of a word.
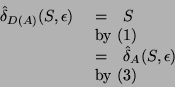

We note that in the step marked with (*) we use a property of
![]() which requires another lemma:
which requires another lemma:
We can now use the lemma to show
Proof:
