Translating regular expressions to NFAs

Theorem 3.1   For each regular expression $E$ we can construct ab NFA $N(E)$ s.t. $L(N(E)) = L(E)$, i.e. the automaton accepts the language described by the regular expression.

Proof:

We do this again by induction on the syntax of regular expressions:

1. $N(\emptyset)$:

   

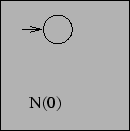
   which will reject everything (it has got no final states) and hence

   $$L(N(\emptyset)) = \emptyset$$

   $$= L(\emptyset)$$

   
   

2. $N(\epsilon)$:

   

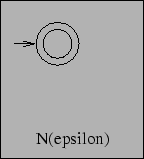
   This automaton accepts the empty word but rejects everything else, hence:

   $$L(N(\epsilon)) = \{\epsilon\}$$

   $$= L(\epsilon)$$

   
   

3. $N(\textbf{x})$:

   

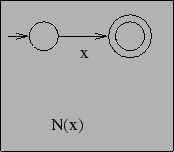
   This automaton only accepts the word x, hence:

   $$L(N(\textbf{x})) = \{ \textrm{x} \}$$

   $$= L(\textbf{x})$$

   
   

4. $N(E+F)$:

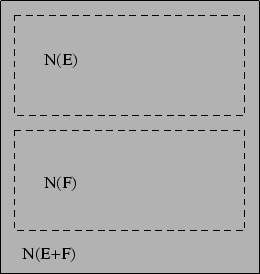
   We merge the diagrams for $N(E)$ and $N(F)$ into one:

   

   I.e. given

   $$N(E) = (Q_E,\Sigma,\delta_E,S_E,F_E)$$

   $$N(F) = (Q_F,\Sigma,\delta_F,S_F,F_F)$$

   
   
   Now we use the disjoint union opration on sets (hope you still remember from MCS), otherwise see pp.55 in the G51MCS notes.

   $$Q_{E+F} = Q_E + Q_F$$

   $$\delta_{E+F}((0,q),x) = \{ (0,q') \mid q' \in \delta_E(q,x) \}$$

   $$\delta_{E+F}((1,q)),x = \{ (1,q') \mid q' \in \delta_F(q,x) \}$$

   $$S_{E+F} = S_E + S_F$$

   $$F_{E+F} = F_E + F_F$$

   $$N(E+F) = (Q_{E+F},\Sigma,\delta_{E+F},S_{E+F},F_{E+F})$$

   
   
   The disjoint union just signals that we are not going to identify states, even if they accidently happen to have the same name.

   Just thinking of the game with markers you should be able to convince yourself that

   $$L(N(E+F)) = L(N(E)) \cup L(N(F))$$

   Moreover to show that

   $$L(N(E+F)) = L(E+F)$$
   we are allowed to assume that

   $$L(N(E)) = L(E)$$

   $$L(N(F)) = L(F)$$

   
   
   that's what is meant by induction over the syntax of regular expressions.

   Now putting everything together:

   $$L(N(E+F)) = L(N(E)) \cup L(N(F))$$

   $$= L(E) \cup L(F)$$

   $$= L(E+F)$$

   
   

5. $N(EF)$:

   We want to put the two automata $N(E)$ and $N(F)$ in series. We do this by connecting the final states of $N(E)$ with the initial states of $N(F)$ in a way explained below.

   

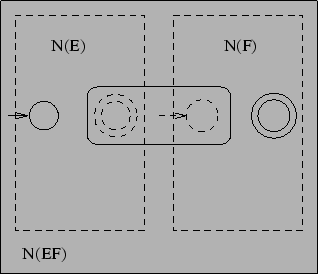
   In this diagram I only depicted one initial and one final state of each of the automata although they may be several of them.

   Here is how we construct $N(EF)$ from $N(E)$ and $N(F)$:

   $$N(E) = (Q_E,\Sigma,\delta_E,S_E,F_E)$$

   $$N(F) = (Q_F,\Sigma,\delta_F,S_F,F_F)$$

   
   
   • The states of $N(EF)$ are the disjoint union of the states of $N(E)$ and $N(F)$:
     $$Q_{EF} = Q_E + Q_F$$

   • The transition function of $N(EF)$ contains all the transitions of $N(E)$ and $N(F)$ (as for $N(E+F)$) and for each pair of a final state $q$ of $N(E)$ and an initial state $q'$ of $N_F$ we add all the arrows coming out of $q'$ to $q$.

     $$\delta_{EF}((0,q),x) = \{ (0,q') \mid q' \in \delta_E(q,x) \}$$

     $$\quad \cup \{ (1,q') \mid q\in F_E \wedge \exists q''\in S_F.q'\in \delta_F(q'',x) \}$$

     $$\delta_{EF}((1,q)) = \{ (1,q') \mid q' \in \delta_F(q)) \}$$

     
     

   • The initial states of $N(EF)$ are the initial states of $N(E)$, and the initial states of $N(F)$ if there is an initial state of $N(E)$ which is also a final state.
     $$S_{EF} = \{ (0,q) \mid q\in S_E \} \cup \{ (1,q) \mid q\in S_F \wedge S_E\cap F_E \not=\emptyset \}$$

   • The final states of $N(EF)$ are the final states of $N(F)$.
     $$F_{EF} = \{ (1,q) \mid q\in F_F \}$$

   We now set
   $$N(EF) = (Q_{EF},\Sigma,\delta_{EF},S_{EF},Z_{EF})$$

   I hope that you are able to convince yourself that

   $$L(N(EF)) = \{ uv \mid u\in L(N(E)) \wedge v\in L(N(F))$$
   and hence we can reason

   $$L(N(EF)) = \{ uv \mid u\in L(N(E)) \wedge v\in L(N(F)) = \{ uv \mid u\in L(E) \wedge v\in L(F)$$

   $$= L(EF)$$

   
   

6. $N(E^*)$:

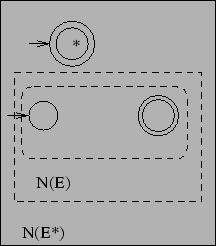
   We construct $N(E^*)$ from $N(E)$ by merging initial and final states of $N(E)$ in a way similar to the previous construction and we add a new state $*$ which is initial and final.

   

   Given

   $$N(E) = (Q_E,\Sigma,\delta_E,S_E,F_E)$$

   
   
   we construct $N(E^*)$.
   • We add one extra state $*$:
     $$Q_{E^*} = Q_E + \{ * \}$$

   • ${N_E}^*$ inherits all transitions form $N_E$ and for each state which has an arrow to the final state labelled $x$ we also add an arrow to all the initial states labelled $x$.

     $$\delta_{E^*}((0,q),x) = \{ (0,q') \mid q' \in \delta_E(q,x) \}$$

     $$\cup (0,q') \mid \exists \delta_E(q,x)\cap F_E \not= \emptyset \wedge q' \in S_E \}$$

     
     

   • The initial states of $N(E^*)$ are the initial states of $N(E)$ and $*$:
     $$S_{E^*} = \{ (0,q) \mid q\in S_E \} \cup \{ (1,*) \}$$

   • The final states of $N_{E^*}$ are the final states of $N_E$ and $*$:
     $$F_{E^*} = \{ (0,q) \mid q\in F_E \} \cup \{ (1,*) \}$$

   We define
   $$N(E^*) = (Q_{E^*},\Sigma,\delta_{E^*},S_{E^*},F_{E^*})$$

   We claim that

   $$L(N(E^*)) = \{ w_0w_1\dots w_{n-1} \mid n\in\mathbb{N}\wedge \forall i<n. w_i \in L(N(E)) \}$$
   since we can run through the automaton an arbitrary number of times. The new state $*$ allows us also to accept the empty sequence. Hence:

   $$L(N(E^*)) = \{ w_0w_1\dots w_{n-1} \mid n\in\mathbb{N}\wedge \forall i<n. w_i \in L(N(E)) \}$$

   $$= L(N(E))^*$$

   $$= L(E)^*$$

   $$= L(E^*)$$

   
   

7. $N(\textbf{(}E\textbf{)}) = N(E)$

   I.e. using brackets does not change anything.

$\Box$

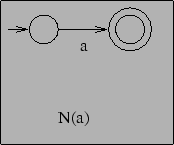
As an example we construct $N(\textrm{a}^*\textrm{b}^*)$. First we construct $N(\textbf{a})$:

Now we have to apply the $*$-construction and we obtain:

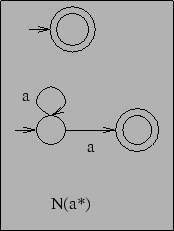
$N(b^*)$ is just the same and we get

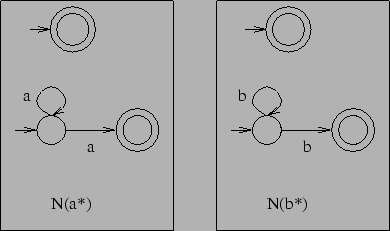
and now we have to serialize the two automata and we get:

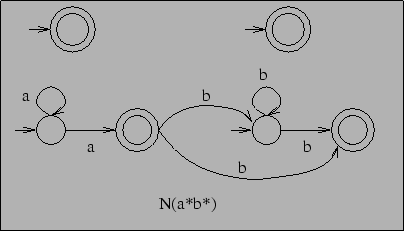
Now, you may observe that this automaton, though correct, is unnecessary complicated, since we could have just used

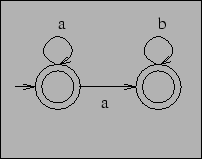
However, we shall not be concerned with minimality at the moment.