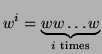Next: Translating regular expressions to
Up: Regular expressions
Previous: What are regular expressions?
The meaning of regular expressions
We now know what regular expressions are but what do they mean?
For this purpose, we shall first define an operation on languages
called the Kleene star. Given a language
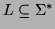 we define
we define
Intuitively, 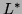 contains all the words which can be formed by
concatenating an arbitrary number of words in
contains all the words which can be formed by
concatenating an arbitrary number of words in 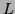 . This includes
the empty word since the number may be 0.
. This includes
the empty word since the number may be 0.
As an example consider
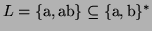 :
:
You should notice that we use the same symbol as in
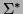 but there is a subtle difference:
but there is a subtle difference: 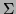 is a set of
symbols but
is a set of
symbols but
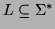 is a set of words.
is a set of words.
Alternatively (and more abstractly) one may describe 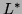 as the
least language (wrt
as the
least language (wrt 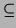 ) which contains
) which contains 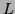 and the empty word
and is closed under concatenation:
and the empty word
and is closed under concatenation:
We now define the semantics of regular expressions: To each regular
expression 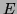 over
over 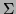 we assign a language
we assign a language
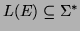 .
We do this by induction over the definition of the
syntax:
.
We do this by induction over the definition of the
syntax:
-
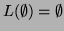
-
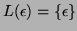
-
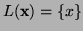
where
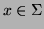 .
.
-
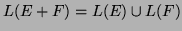
-
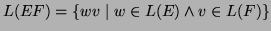
-
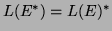
-
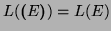
Subtle points: in 1. the symbol 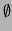 may be used as a regular
expression (as in
may be used as a regular
expression (as in
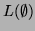 ) or the empty set
(
) or the empty set
(
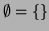 ). Similarily,
). Similarily, 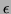 in 2. may be a regular
expression or a word, in 6.
in 2. may be a regular
expression or a word, in 6.  may be used to construct regular
expressions or it is an operation on languages. Which alternative we mean
becomes only clear from the context, there is no generally agreed
mathematical notation
1to make this difference explicit.
may be used to construct regular
expressions or it is an operation on languages. Which alternative we mean
becomes only clear from the context, there is no generally agreed
mathematical notation
1to make this difference explicit.
Let us now calculate what the examples of regular expressions from the
previous section mean, i.e. what are the langauges they define:
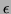
-
By 2.
-
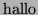
-
Let's just look at
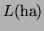 . We know from 3:
. We know from 3:
Hence by 5:
Continuing the same reasoning we obtain:
-
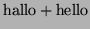
-
From the previous point we know that:
Hence by using 4 we get:
-
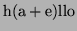
-
Using 3 and 4 we know
Hence using 5 we obtain:
-
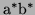
-
Let us introduce the following notation:
Now using 6 we know that
and hence using 5 we conclude
I.e.
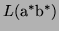 is the set of all words which start
with a (possibly empty) sequence of as followed by a
(possibly empty) sequence of bs.
is the set of all words which start
with a (possibly empty) sequence of as followed by a
(possibly empty) sequence of bs.
-
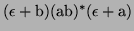
-
Let's analyze the parts:
Hence, we have
In english:
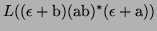 is
the set of (possibly empty) sequences of interchanging as and bs.
is
the set of (possibly empty) sequences of interchanging as and bs.



Next: Translating regular expressions to
Up: Regular expressions
Previous: What are regular expressions?
Thorsten Altenkirch
2001-05-08
![]() we define
we define
![]() :
:
![]() but there is a subtle difference:
but there is a subtle difference: ![]() is a set of
symbols but
is a set of
symbols but
![]() is a set of words.
is a set of words.
![]() as the
least language (wrt
as the
least language (wrt ![]() ) which contains
) which contains ![]() and the empty word
and is closed under concatenation:
and the empty word
and is closed under concatenation:
![]() over
over ![]() we assign a language
we assign a language
![]() .
We do this by induction over the definition of the
syntax:
.
We do this by induction over the definition of the
syntax:
![]() . We know from 3:
. We know from 3: